CS Notes

Searching Algorithms

4 min read

Searching Algorithms

What is a searching algorithm?

  • A searching algorithm is a method to find a specific value or element within a data structure.
  • The two most common are:
    • Binary search
    • Linear search
  • The linear search is a standard algorithm used to find elements in an unordered list. The list is searched sequentially and systematically from the start to the end one element at a time, comparing each element to the value being searched for
    • If the value is found the algorithm outputs where it was found in the list
    • If the value is not found it outputs a message stating it is not in the list
  • An example of using a linear search would be looking for a specific student name in a list or searching for a supermarket item in a shopping list

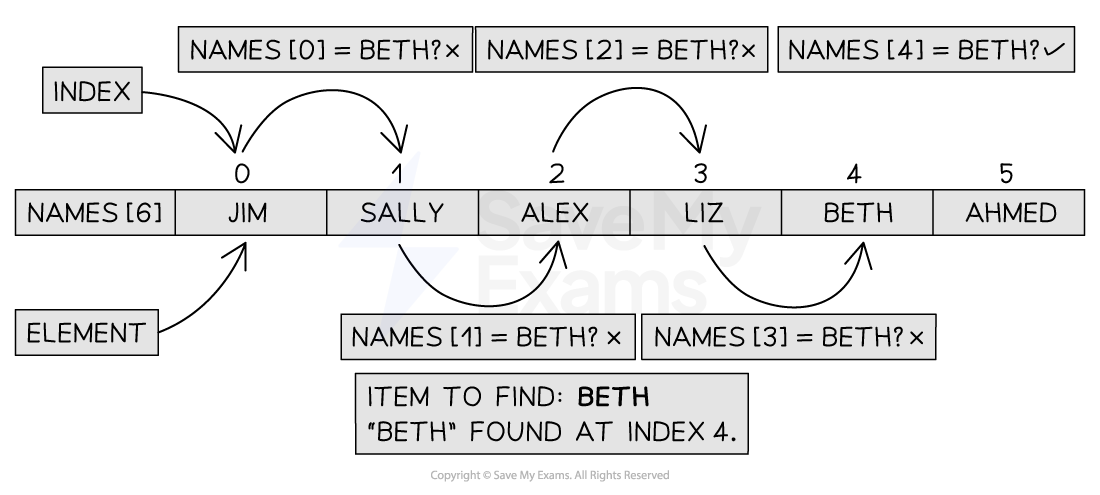figure-1--performing-the-linear-search-revision-notes-computer-science Figure 1: Performing the Linear Search

  • To determine the algorithm’s execution time as measured by the number of instructions or steps carried out, Big-O notation must be used
  • The loop is executed n times, once for each item. There are two instructions within the loop, the if statement and an assignment, hence the Big-O for the loop is O(2n)
  • There are three initial statements which are O(1)
  • The overall Big-O notation is therefore 2n + 3, which when coefficients are factored out, becomes O(n) as linear time dominates constant time. The constant term and coefficients contribute significantly less as the input size n grows larger
  • It is important to remember here that O(n) is the worst case scenario. The best case scenario O(1) would find the item the first time, while the average case would be O(n/2) which when we remove coefficients still becomes O(n)
  • Linear search has a space complexity of O(1) because it does not require any additional memory that grows with the size of the input
  • It only uses a constant amount of extra space, such as a loop counter or a variable to store the target value
  • Given the following list [5, 4, 7, 1, 3, 8, 9, 2], a trace table for the linear search is shown below

Trace Table of the Linear Search

itemindexilist[i]found
8-105False
14
27
31
43
8558True

Pseudocode

function linearSearch(list, item)
	index = -1
	i = 0
	found = False
	while i < len(list) and found = False
		if list[i] = item then
			index = i
			found = True
		endif
		i = i + 1
	endwhile
	return index
endfunction
  • In the above algorithm, a list of n ordered items is passed to the function and three variables are initialised
  • index = -1 is a default value to indicate “not found”, i = 0 is a counter to ensure the loop starts at the beginning of the list and found = False sets a flag to track when/if the value you are searching for is found
  • The loop continues as long as the counter hasn’t reached the end of the list and if list[i] = item the current index is stored as the location of the item
  • The flag **found **is set to True to signal the search can be stopped
  • i = i + 1 increments the counter to **move to the next element **in the list if the value is not found
  • After the loop completes the function returns the final value of index

Python

def linear_search(list, item):
    index = -1
    for i in range(len(list)):
        if list[i] == item:
            index = i
            break  # Stop the loop once the item is found
    return index

Java

public class LinearSearch {
    public static int linearSearch(int[] list, int item) {
        int index = -1;
        for (int i = 0; i < list.length; i++) {
            if (list[i] == item) {
                index = i;
                break;  // Stop the loop once the item is found
            }
        }
        return index;
    }
}

Graph View

Backlinks