Karnaugh Maps

Karnaugh Maps

What is a Karnaugh map?

• In A Level Computer Science, a Karnaugh map is a tool that is used for simplifying Boolean algebra expressions
• It offers a visual method of grouping together expressions with common factors
• The format of the map makes it easy to identify and eliminate redundant terms
• They are used in digital logic design, such as simplifying the logic of digital circuits

Steps

1. Create the Map: Each cell in the grid corresponds to a term in the Boolean expression. Fill cells with 1s and 0s corresponding to the output of that term
2. Grouping: Group the 1s in the grid. Each group must be a rectangle and the size of the group must be a power of 2. A cell can be part of multiple groups
3. Simplifying: Write down a simplified Boolean expression for each group. The simplified expression for a group consists of the variables that remain constant in all terms in the group
4. Final Expression: Combine the simplified expressions from each group using OR operations to get the final simplified Boolean expression

Creating Karnaugh Maps

• A Karnaugh Map (KMap) can be used to simplify a Boolean expression with 2 inputs
• Here is an example for the expression A V B (A OR B)

Step 1

• Add each variable starting with A at the top and B down the side
• Add each possible state for A and B

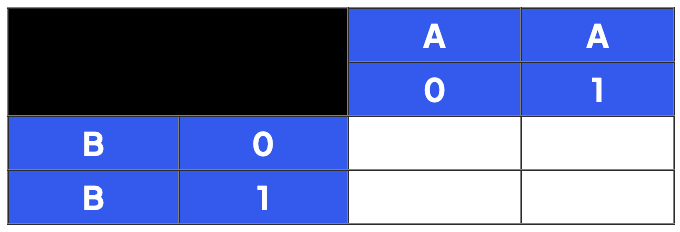step 1

Step 2

• Take each expression in turn separated by the V (OR)
• First look at A on it’s own
• Find all cells where A is 1
• Add 1 to the cell

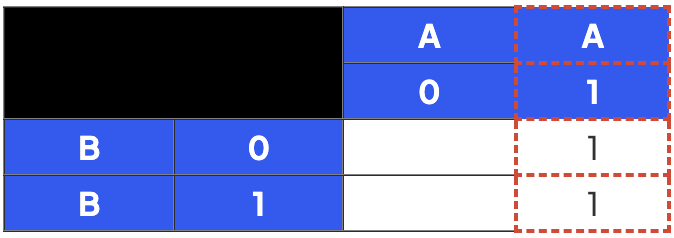step 2

Step 3

• Repeat for B

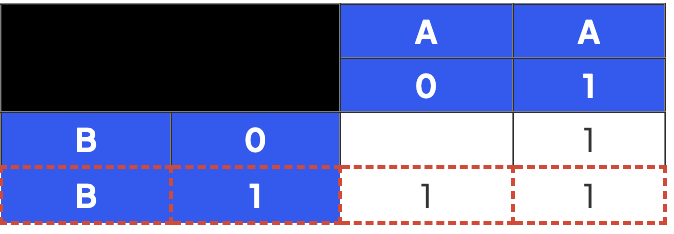step 3

Step 4

• This is now a completed KMap for the expression A V B (A OR B)

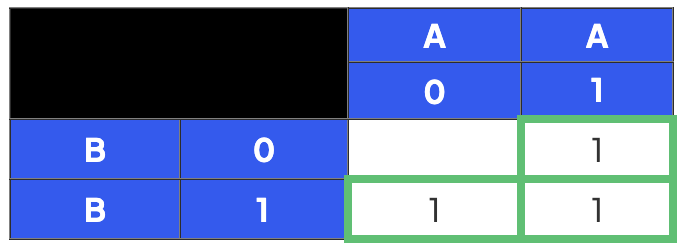step

Simplifying Expressions Using Karnaugh Maps

Simplify $\neg A\wedge \neg B\wedge C\vee \neg A\wedge B\wedge \neg C\vee A\wedge \neg B\wedge C\vee A\wedge B$ using a KMap.

In this example there will be 3 variables A,B and C so the empty KMap will look like this:

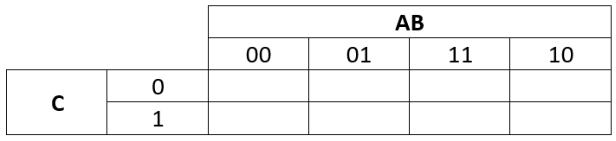empty-k-map

Step 1

Split this long term at each OR giving 4 smaller expressions (subterms) to add to the table:

• $\neg A\wedge \neg B\wedge C$
• $\neg A\wedge B\wedge \neg C$
• $A\wedge \neg B\wedge C$
• $A\wedge B$

Step 2

• Take the first subterm $\neg A\wedge \neg B\wedge C$
• Put a 1 in the map for every cell where this term would be TRUE (1)
• So if A and B were 0 and C was 1 this subterm would be 1
• So put a 1 in every cell in the KMap where A is 0, B is 0 and C is 1

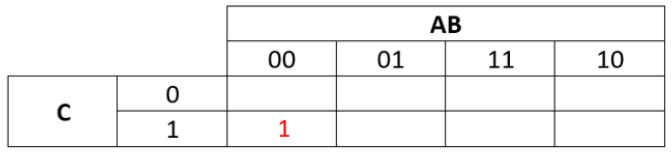k-map-2

Step 3:

• The next subterm is $\neg A\wedge B\wedge \neg C$
• Put a 1 in the KMap where A is 0, B is 1 and C is 0

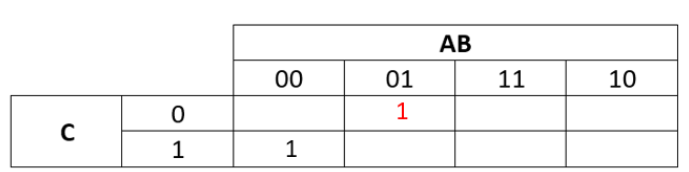k-map-3

Step 4:

• The next subterm is $A\wedge \neg B\wedge C$
• Put a 1 in the KMap where A is 1, B is 0 and C is 1

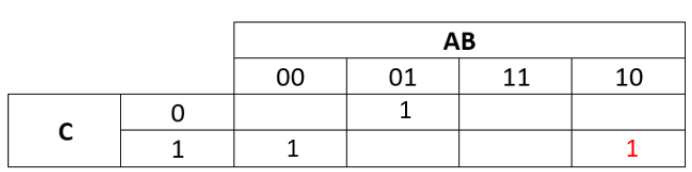k-map-4

Step 5:

• The final subterm is $A\wedge B$
• Put a 1 in the KMap where A is 1 and B is 1 (2 cells this time)

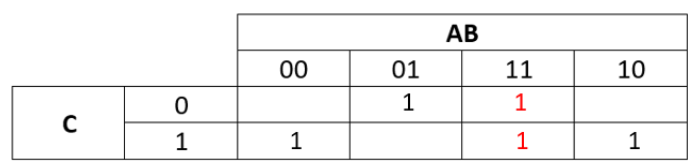k-map-5

Making the groups

• Once you have written the 1s and 0s into your KMap, you can then use this to simply the expression
• In order to do this, you need to identify the groups
• This is the key to using the Karnaugh map to derive the simplified expression
• The aim of making the groups is to
  • Make rectangular groups
  • Make groups that are as large as possible
  • Make groups that contain either 8,4,2 or 1 ones
  • Groups can overlap (i.e. some ones can be in multiple groups)
  • The Karnaugh map ‘grid’ wraps round in all directions so the groups can wrap round

Example grouping

Group 1:

So this would be one group.

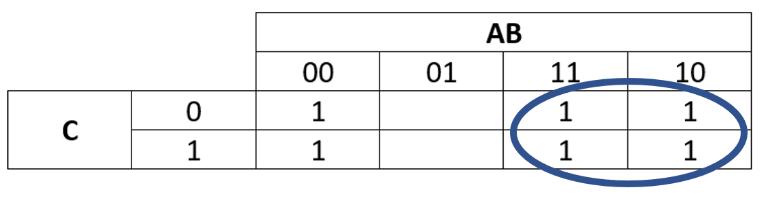k-map-6

This group would represent $A$ since within this group both $C$ and $B$ change (have zeros and ones) whereas for $A$ all the cells are one.

Group 2:

This would be another group (note the wrapping around).

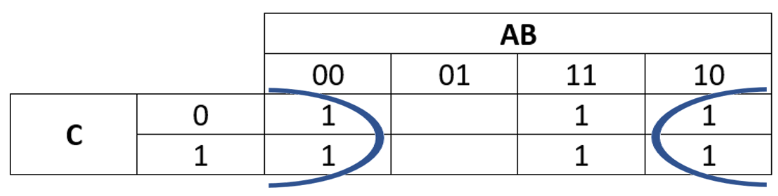k-map-7

This group would represent $\neg B$ since within this group both $A$ and $C$ change (have zeros and ones) whereas for $B$ all the cells are zero

Final simplified expression

• To get the final simplified expression we OR the terms representing the two groups together.
• So the simplified expression is $A\vee \neg B$

Examiner Tips and Tricks

In questions where you have to use a Karnaugh Map always show the groups by drawing a box/circle round them.

Worked Example

A Boolean expression is entered into a Karnaugh map.

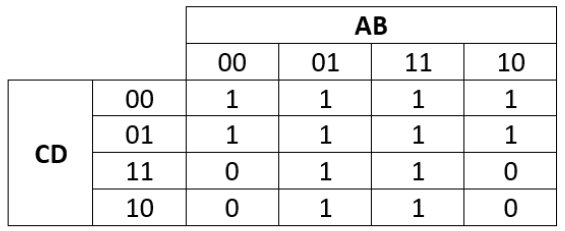k-map-8

Give a simplified version of the expression using the Karnaugh map.

You must show your working

[3 marks]

How to answer this question:

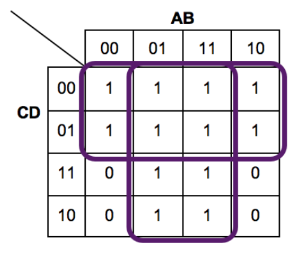k-map-9

• Looking at the group of 8 in the middle of the map, for all the cells in the group the variable $B$ is always a 1
• The 3 other variables change across the group (i.e. for some cells they are 0 and for others they are 1
• So this group is $B$
• Looking at the other group of 8, for all the cells in this group, $C$ is always 0 but the other 3 variables can be 1 or 0 in this group So this group simplifies to $\neg C$

Answer that gets full marks:

$B\vee \neg C$