Graphs
What is a Graph?
- A graph is a set of vertices/nodes that are connected by edges/pointers. Graphs can be placed into the following categories:
- Directed Graph: The edges can only be traversed in one direction
- Undirected Graph: The edges can be traversed in both directions
- Weighted Graph: A value is attached to each edge
Computers are able to process graphs by using either an adjacency matrix or an adjacency list.
The examples below will be illustrated using an adjacency matrix, more information on programming using both matrices and lists is available in section 8.
Undirected, Unweighted Graph
For unweighted graphs:
- 1 is set when an edge exists between 2 nodes
- 0 is set when there is no edge between 2 nodes
Below is the adjacency matrix for an undirected, unweighted graph:
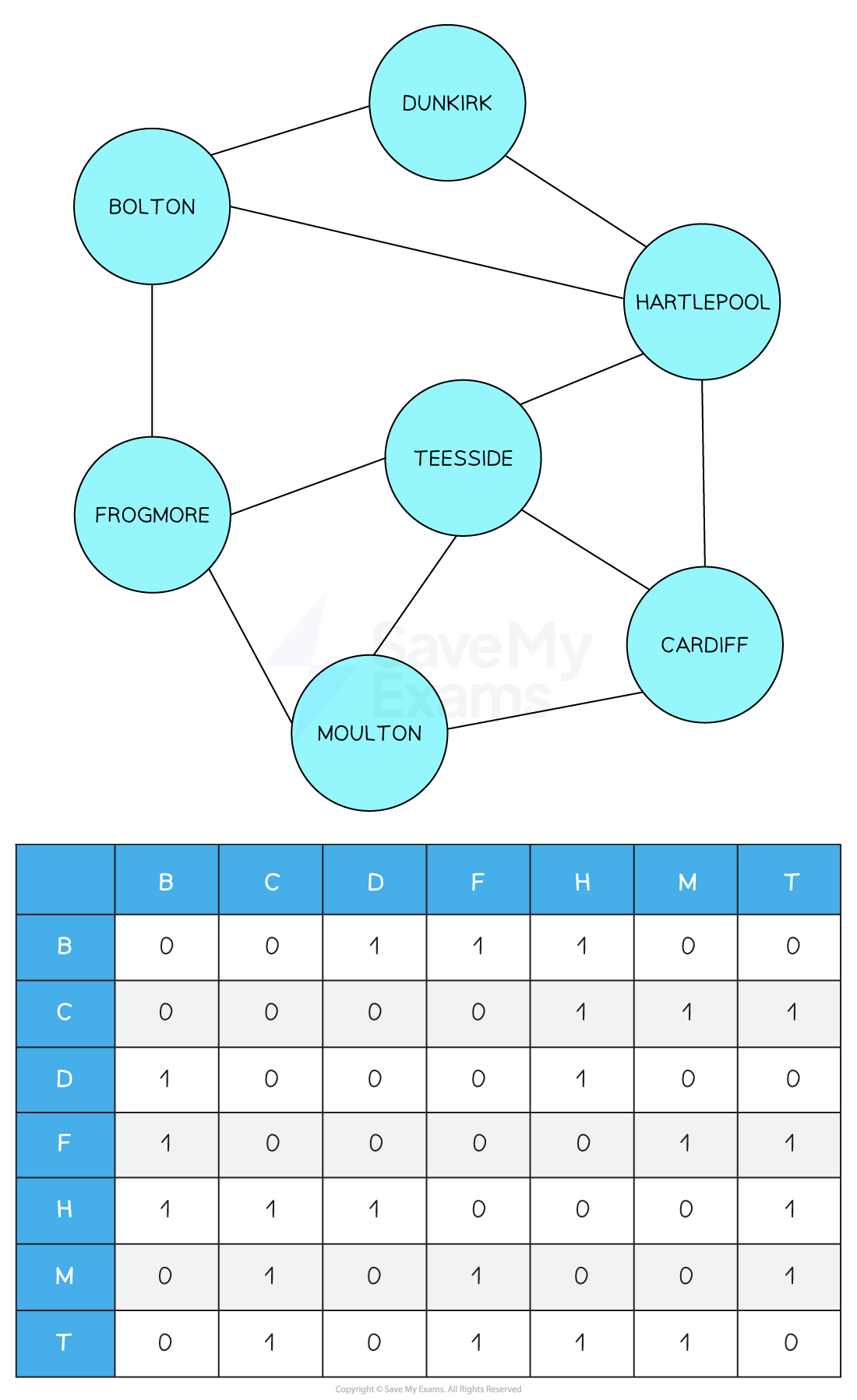
For this graph, the names are abbreviated to the first letter.
- The data in an adjacency matrix for an unweighted graph is symmetric
- To determine the presence or absence of an edge, you inspect the row (or column) that represents a node. Example: If you wanted to see if there is an edge between Frogmore and Hartlepool you can look at the cross-section of row 3 (for Frogmore) and column 4 (for Hartlepool)
- You need a method (e.g Dictionary) to record which row/column is used for a specific node’s edge data
- The data values for the nodes (in this example names of towns) are not stored in the matrix
Directed, Unweighted Graph
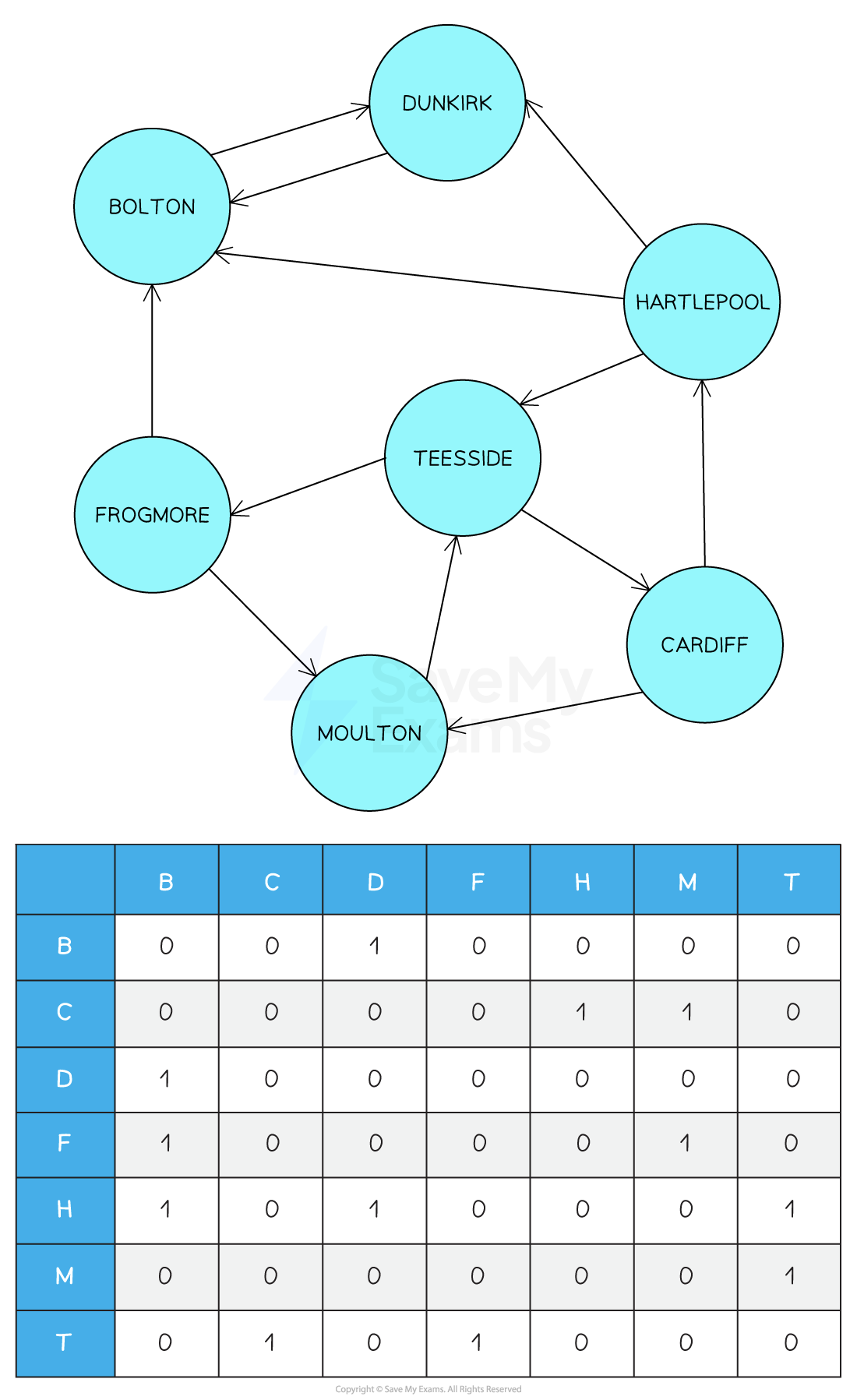
Above is the adjacency matrix for a directed, unweighted graph. For this graph, the names are abbreviated to the first letter.
- Due to the lack of symmetry in this matrix, you cannot access the data by both row and column, you must know the direction in which the values are stored
- E.g.: In row 0 for Bolton there is only one neighbour (Dunkirk) because there is a single directed edge from Bolton towards Dunkirk. This is because there are 3 edges directed towards Bolton (from Dunkirk, Hartlepool and Frogmore)
- If you are implementing a graph as an adjacency matrix you will need to choose the direction and make sure that the data is stored and accessed correctly
Undirected, Weighted Graph
- For weighted graphs the values of the weights are stored in the adjacency matrix
- If an edge does not exist between two nodes, then a very large number (normally the infinity symbol ∞) is set
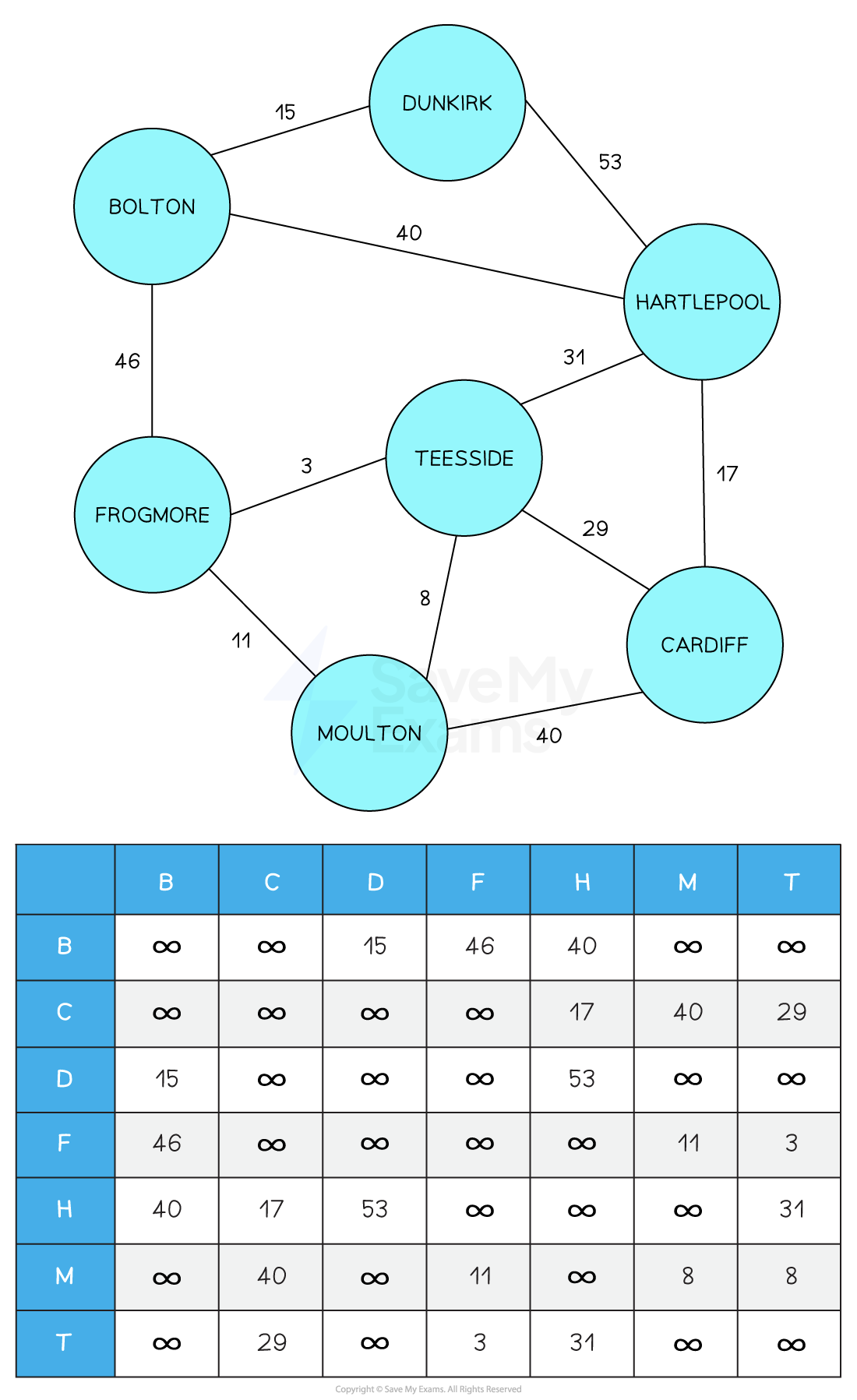
Above is the adjacency matrix for an undirected, unweighted graph. For this graph, the names are abbreviated to the first letter.
Directed, Weighted Graph
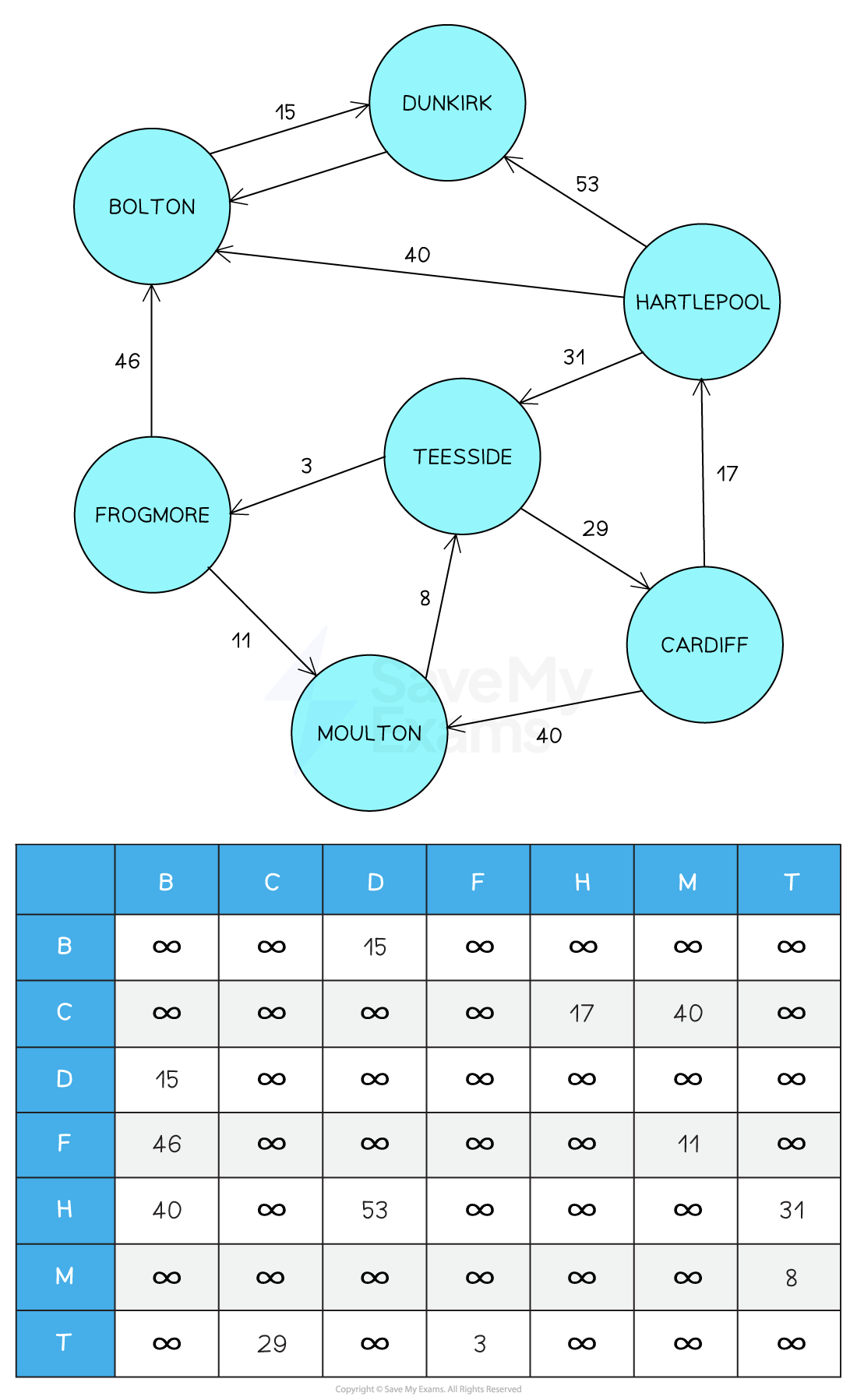
Above is the adjacency matrix for a directed weighted graph: For this graph, the names are abbreviated to the first letter.
The Applications of Graphs
Graphs have many uses in the world of Computer Science, for example:
- Social Networks
- Transport Networks
- Operating Systems
| Keyword | Definition |
|---|---|
| Directed Graph | A directed graph is a set of objects that are connected together, where the edges are directed from one vertex to another. |
| Undirected Graph | An undirected graph is a set of objects that are connected together, where the edges do not have a direction. |
| Weighted Graph | A weighted graph is a set of objects that are connected together, where a weight is assigned to each edge. |
| Adjacency Matrix | Also known as the connection matrix is a matrix containing rows and columns which is used to present a simple labelled graph. |
| Adjacency List | This is a collection of unordered lists used to represent a finite graph. |
| Vertices/Nodes | A vertex (or node) of a graph is one of the objects that are connected. |
| Edges/Arcs | An edge (or arc) is one of the connections between the nodes (or vertices) of the network. |
| Dictionary | A collection of names, definitions, and attributes about data elements that are being used or captured in a database, information system, or part of a research project. |
TIP
Examiner Tips and Tricks
It is not important what the graph looks like, but which vertices are connected.